Figure 21. Find Angles A and B, and Side "B"

Machine Shop Calculation
Page Navigation
72

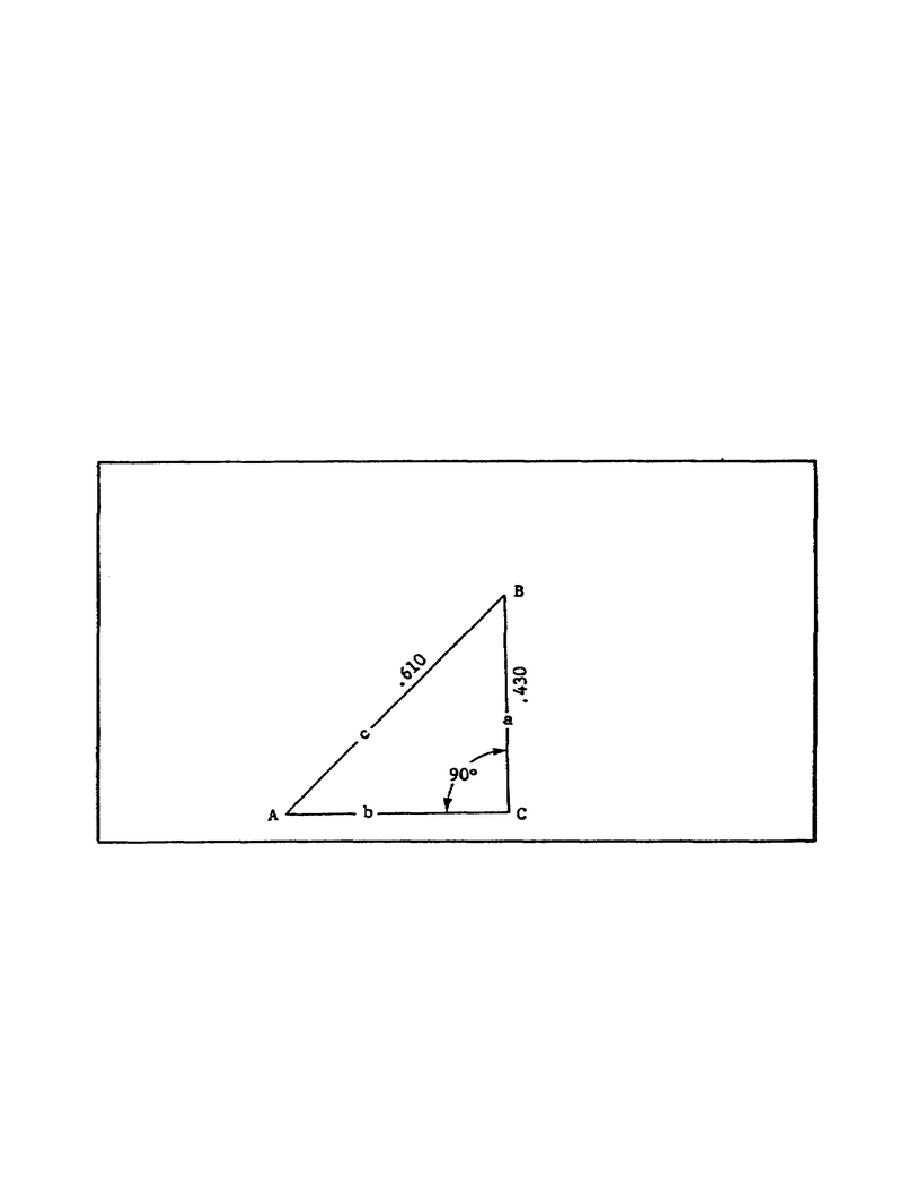
Given the hypotenuse and one side, find the angles A and B, and side "b" of

figure 21.

SOLUTION

Here, "b" is the side adjacent. According to rule (1)(see page 53), sin A =

side opposite ƒ hypotenuse.

Substituting .430 for side opposite and .610

for hypotenuse, sin A = .430 ƒ .610 = .70492.

Therefore, A = 44,, 49' 23" and B = 90,, - A = 45,, 10' 37". According to rule

8, side adjacent = hypotenuse x cosine.

Substituting .610 for hypotenuse

and .7093 for cosine, we get: side adjacent = .610 x .7093 = 4327.

FIGURE 21.

FIND ANGLES A AND B, AND SIDE "B."

EXAMPLE

Given two sides (figure 22 on the following page), find angles A and B, and

side "c."

SOLUTION

According to rule (3)(see page 53), tan A = side opposite ƒ side adjacent.

Substituting .360 for side opposite and .250 for side adjacent,