MACHINE SHOP CALCULATION - OD1640 - LESSON 2/TASK 3
EXAMPLE
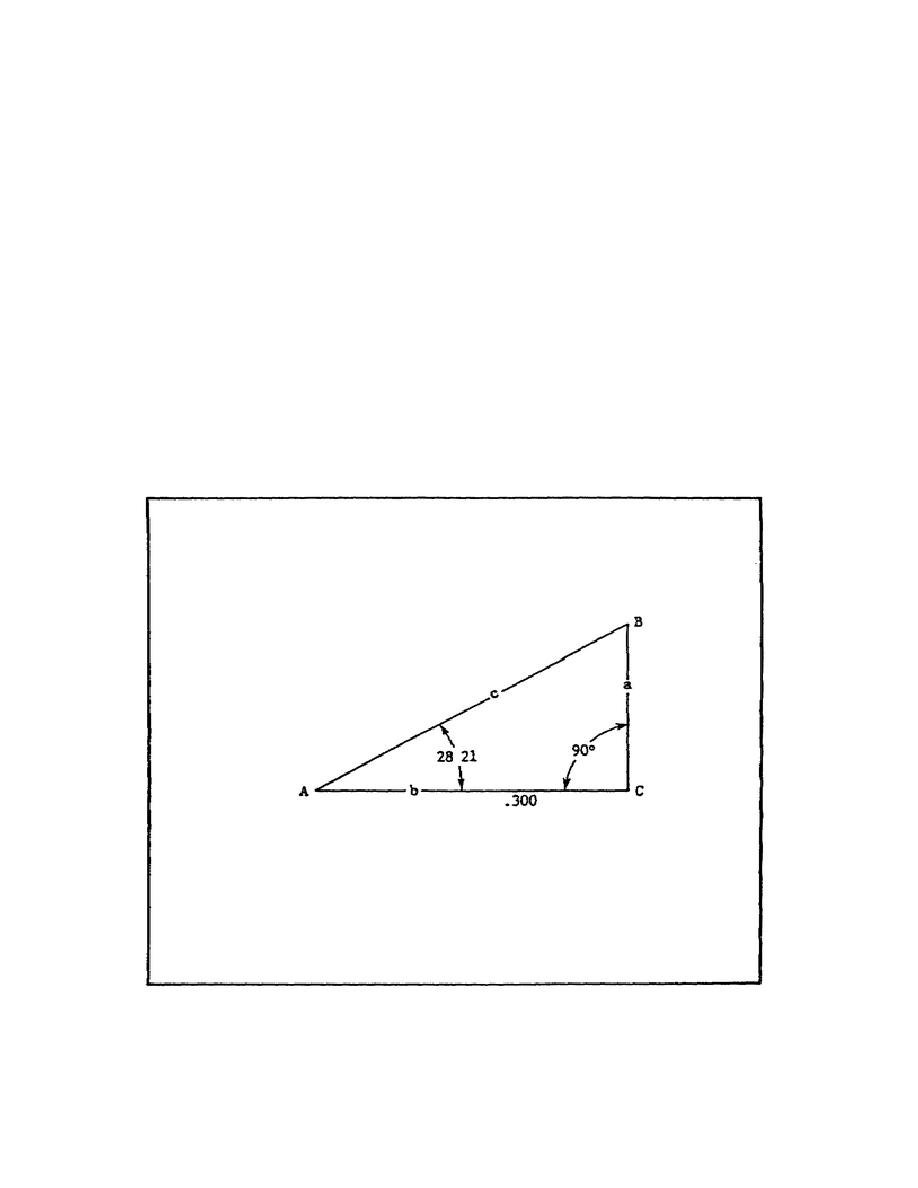
Given an acute angle and adjacent side in figure 20, find angle B and sides
"a" and "c."
SOLUTION
Here, "a" is the side opposite and "c" is the hypotenuse. Angle B = 90,, - A
= 61,, 39'.
According to rule (6)(see page 53), side opposite = side
adjacent ƒ tangent, or rule (7)(see page 53), side opposite = side adjacent
ƒ cotangent. Substituting .300 meters for side adjacent and .5396 for tan,
side opposite = .300 x .5396 = .1619 meter. Or, substituting .300 for side
adjacent and 1.8533 for cotangent, side opposite = .300 ƒ 1.8533 = .1619.
According to rule (12)(see page 54), hypotenuse side adjacent ƒ cosine.
Substituting .300 for side adjacent and .8801 for cosine, hypotenuse = .300
ƒ .8801 = .34087.
FIGURE 20.
FIND ANGLE B AND SIDES "A" AND "C."
70





 Previous Page
Previous Page
