MACHINE SHOP CALCULATION - OD1640 - LESSON 2/TASK 3
angle, two parts are known (at least one of them being a side).
The two
known parts must be either one of the acute angles and any one of the sides,
or any two sides.
EXAMPLE
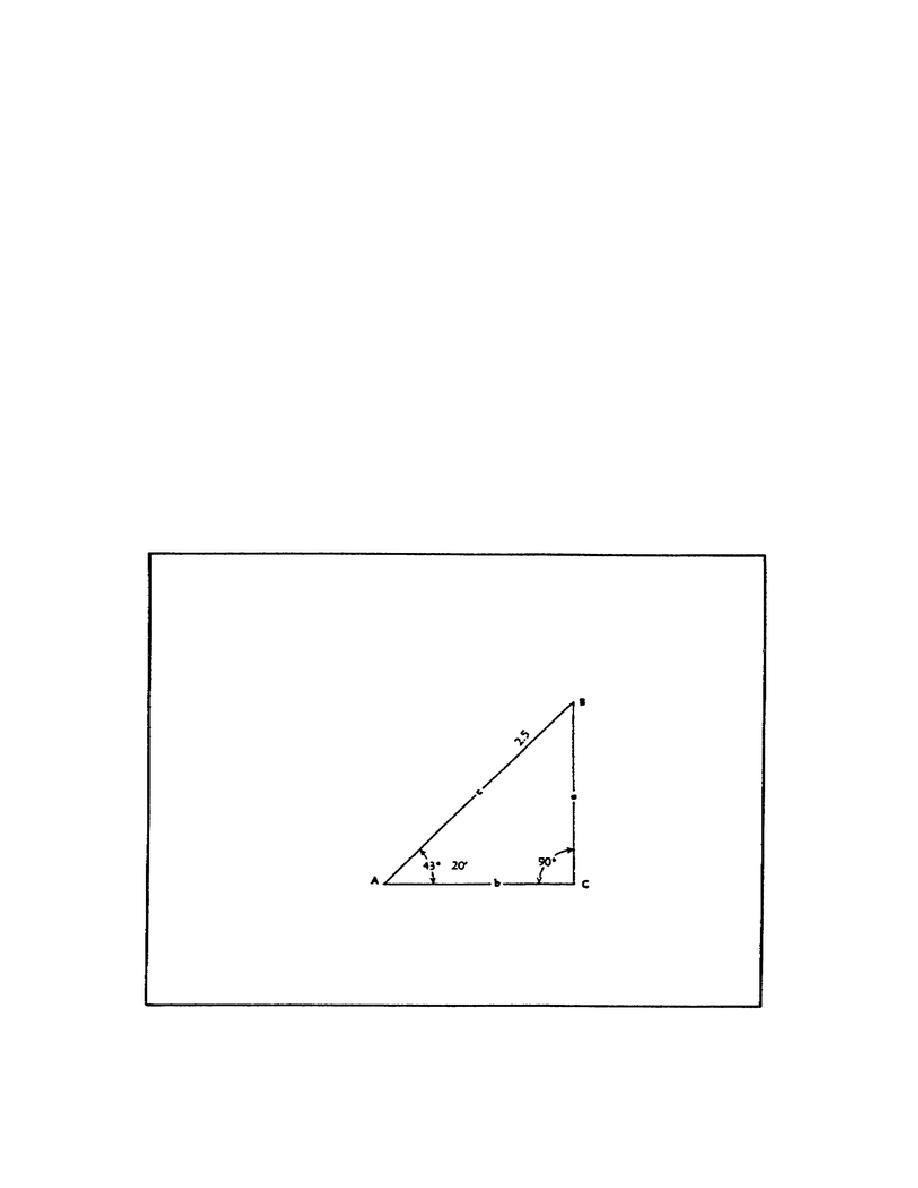
Given an acute angle and the hypotenuse in figure 18, find angle B and sides
"a" and "b."
SOLUTION
Here, "a" is the side opposite and "b" is the side adjacent to Angle A.
Angle B = 90,,- A = 46,, 40', which is the complement of angle A. According
to rule (5)(see page 53), side opposite = hypotenuse x sine. Substituting
2.5 cm for hypotenuse and .6862 for sine, side opposite = 2.5 x .6862- =
1.716 cm. According to rule (8)(see page 53), side adjacent = hypotenuse x
cosine.
... Substituting 2.5 cm for hypotenuse and .7274 for cosine, side
adjacent = 2.5 x .7274 = 1.819.
FIGURE 18.
FIND ANGLE "B" AND SIDES "A" AND "B."
68




 Previous Page
Previous Page
