MACHINE SHOP CALCULATION - OD1640 - LESSON 2/TASK 3
of the formulas which can be derived from the relationship of their sides
and angles. These relationships enable one to make certain substitutions in
the general right triangle rule formula, and to derive certain constants
which hold true no matter what the size the right triangle is, just as long
as its angles are 45,, - 45,, or 30,, - 60,,.
b.
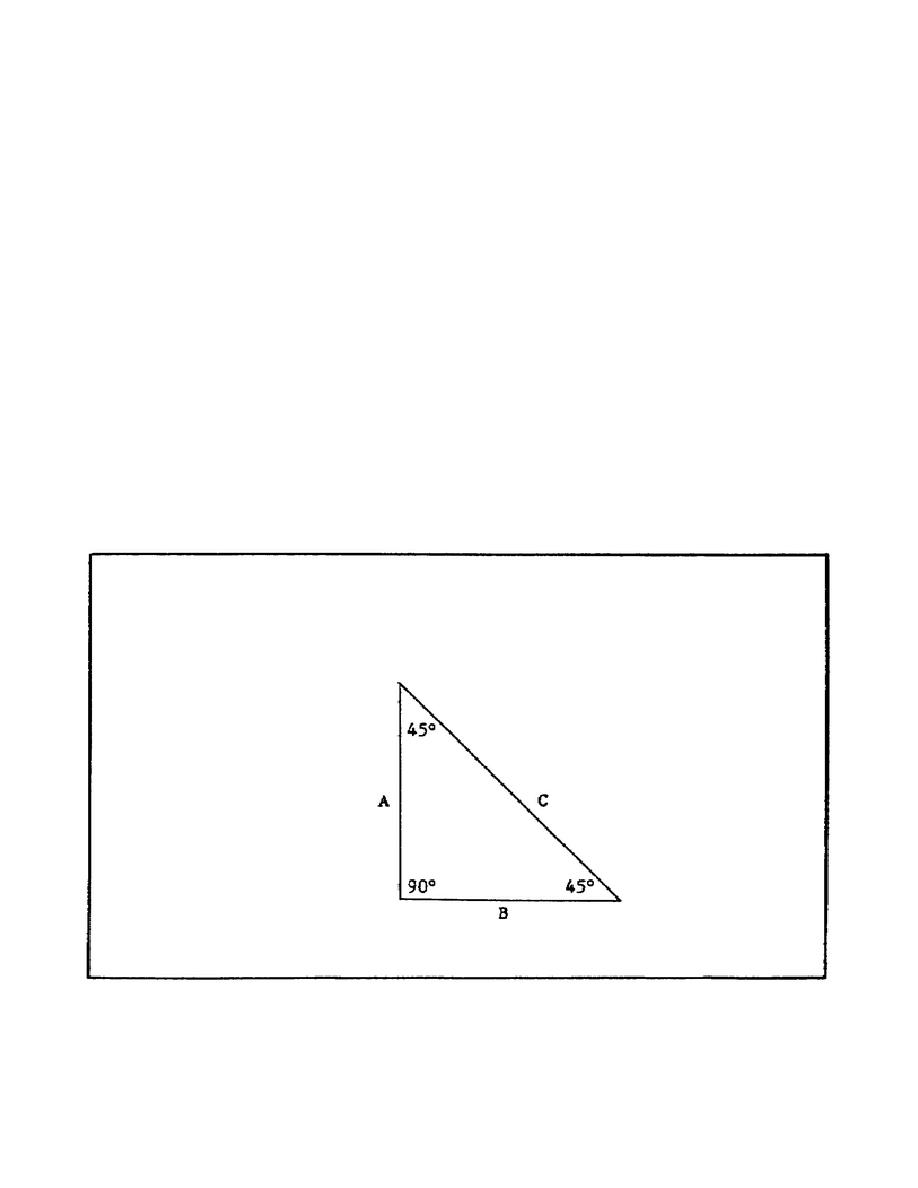
Derivation of the 45,, - 45,, Isosceles Triangle Relationship.
(1) In a 45,, - 45,, right triangle, as in any isosceles triangle, the sides
opposite the equal angles are equal.
Thus, in figure 23, side A can be
substituted for side B.
For example, if side A equals 2 inches, side B
would also equal 2 inches; therefore, the length of the hypotenuse, side C,
could be determined by multiplying the square root of one side by a value of
2.
In the following example we will show how the length of side C, the
hypotenuse, is derived by using side A as described above.
The last two
steps in this procedure serve to demonstrate that once the length of side C
has been found, the length of the two opposite sides can be determined by
multiplying the length of the hypotenuse or side C by the sine of either of
the 45,, angles. The following example demonstrates this process.
FIGURE 23.
FUNCTIONS OF A 45,, ANGLE.
73




 Previous Page
Previous Page
