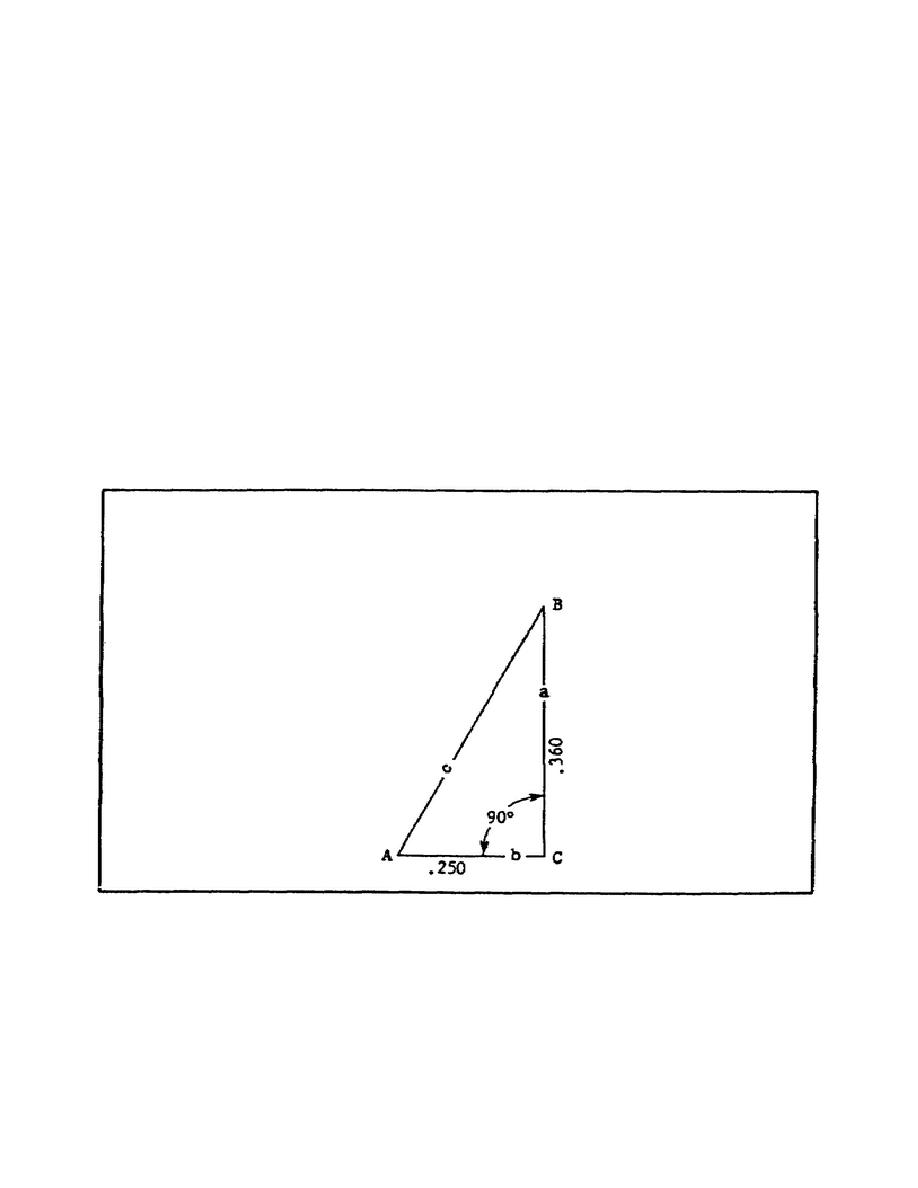
MACHINE SHOP CALCULATION - OD1640 - LESSON 2/TASK 3
tan A = .360 ƒ .250 = 1.44; hence, angle A = 55,, 13' 20", angle B = 34,, 46'
40". According to rule 12, hypotenuse = side adjacent ƒ cosine.
Substituting .250 for side adjacent and .5704 for cosine:
hypotenuse = .250
ƒ .5704 = .4383.
This concludes the processes for solving right triangles. In the following
paragraphs, the process for solving special right triangles will be
described.
Here, the sum of all the angles is 180,,, as in the right
triangles previously discussed.
Special right triangles, however, are
triangles such as the isosceles triangle, which has two 45,, angles at
opposite ends from each other, with the third angle equaling 90,, and,
therefore, has two sides that are of equal length. Thus, 45,, + 45,, + 90,, =
180,,. The other special type of triangle is that which has a 30,, angle and
a 600 on opposite ends from each other, with the third angle equaling 90,,.
Thus, 30,, + 60,, + 90,, = 180,,.
FIGURE 22.
FIND ANGLES A AND B, AND SIDE "C."
9.
Special Right Triangles (45,, - 45,,; 30,, - 60,,)
a.
The isosceles right triangles (two equal sides and two equal angles)
and triangles with a 30,, angle and a 60,, angle are referred to in the
machine shop as "special right triangles" because
72





 Previous Page
Previous Page
