ELECTRONIC PRINCIPLES - OD1647 - LESSON 1/TASK 1
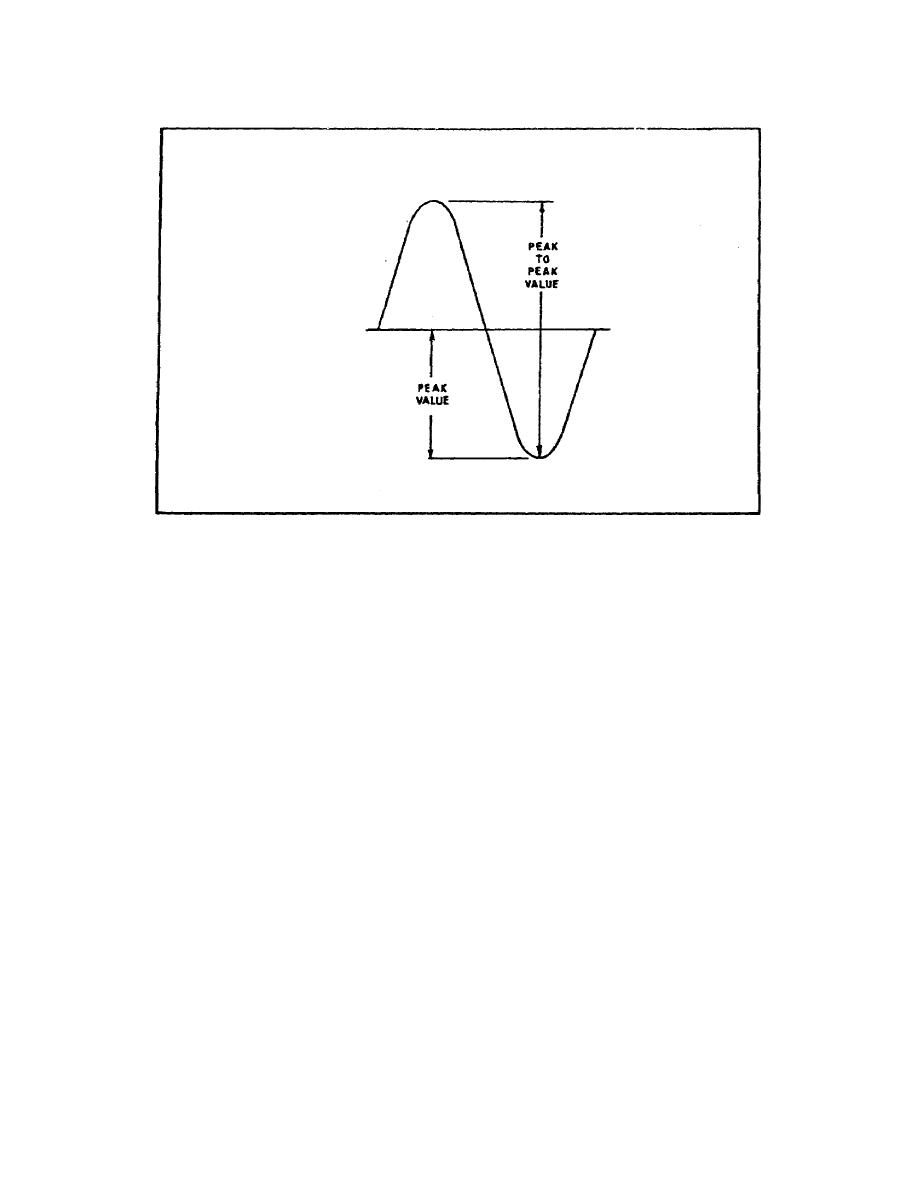
FIGURE 65. PEAK AND PEAKTOPEAK VALUES.
between those two limits. You could determine the average value
by adding together a series of instantaneous values of the
alternation (between 0 and 180), and then dividing the sum by
the number of instantaneous values used. The computation would
show that one alternation of a sine wave has an average value
equal to 0.636 times the peak value. The formula for average
voltage is:
Eavg = 0.636 x Emax
where Eavg is the average voltage of one alternation, and Emax is
the maximum or peak voltage. Similarly, the formula for average
current is:
Iavg = 0.636 x Imax
where Iavg is the average current of one alternation, and Imax is
the maximum or peak current.
Do not confuse the above definition of an average, value with
that of the average value of a complete cycle. Because the
voltage is positive during one alternation and negative during
the other
94





 Previous Page
Previous Page
