MACHINE SHOP CALCULATION - OD1640 - LESSON 2/TASK 2
EXAMPLE
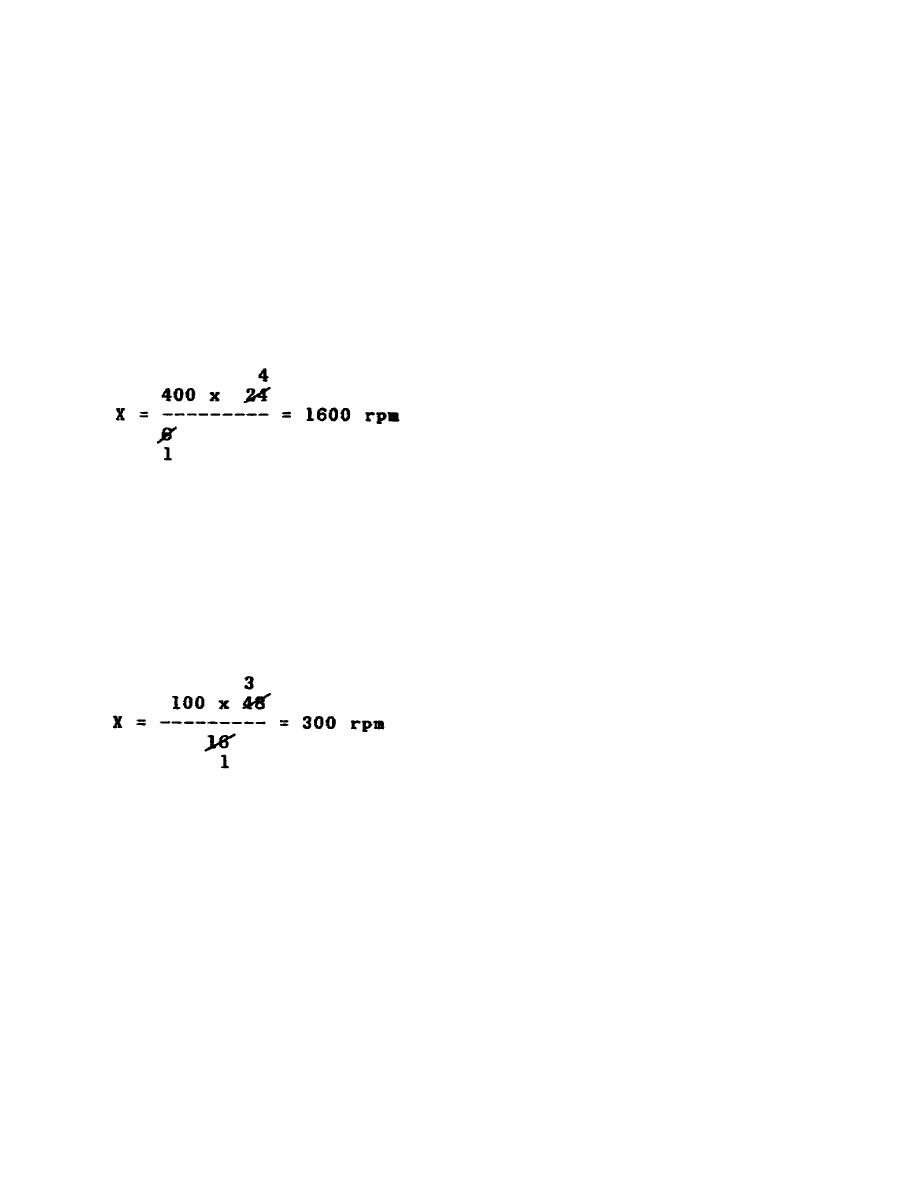
A 24 inch pulley fixed to a live shaft which makes 400 revolutions per
minute (rpm) is belted to a 6 inch pulley, as shown in figure 8 on the
following page. Find the rpm of the smaller pulley.
This is what the problem looks like:
A is the driving pulley, B is the driven pulley.
Then, X : 400 :: 24 : 6
(b) Rule 2.
The speed of gears
running
together
is
inversely
proportional to their number of teeth.
EXAMPLE
A driving gear with 48 teeth meshes with a driven gear which has 16 teeth.
If the driving gear makes 100 rpm, find the number of rpm of the driven
gear.
3.
Pulley Trains and Gear Trains
a.
In the previous paragraph, we discussed the meanings and methods of
solving ratio and proportion problems.
In this paragraph, we will apply
these methods to help determine the size to which a pulley or gear should be
machined in order to enable it to rotate at a given number of revolutions
per minute (rpm) for efficient operation of the machinery pulley train or
vehicle gear train.
A pulley train is a series of pulleys connected by
belting as shown in figure 9 on page 47. A gear train is a series of gears
running
45





 Previous Page
Previous Page
